以一道数学题开始我的发文

废话不多说，直接上题

$https://latex.codecogs.com/svg.image?\iint_D \frac{(x+y) \ln \left(1+\frac{y}{x}\right)}{\sqrt{1-x-y}} \mathrm{d} x \mathrm{d} y$

其中区域D由直线x + y = 1 与两坐标轴所围成得三角形区域。

解:
　　这题的式子较为复杂，直接求解可能计算量偏大，进而考虑其它方法，首先考虑换元法.
　　不妨设：

$https://latex.codecogs.com/svg.image?\left\{\begin{array}{l}x+y=u \\\frac{y}{x}=u\end{array}\right.$

　　解，得：

$https://latex.codecogs.com/svg.image?\left\{\begin{array}{l}x=\frac{u}{1+u} \\y=\frac{u v}{1+v}\end{array}\right.$

　　因为由x, y 两个变量的变换所以我们需要用到隐函数存在定理3的Jacobi行列式，下面

例子.png

【注】设 $https://latex.codecogs.com/svg.image?x=x(u, v), \quad y=y(u, v)$ ，雅可比行列式是:

$https://latex.codecogs.com/svg.image?\mathbf{J}=\left|\frac{\partial(x, y)}{\partial(u, v)}\right|=\left|\begin{array}{ll}x_u & x_v \\y_u & y_v\end{array}\right|$

这只是公式，其条件需要读者自寻理解。(ps：我也是小菜鸟)

（给上书本的定义，我也理解理解）
　　这里有个值得注意的是在积分是dxdy代表的是面积，所以在变换时需要对J加上绝对值,所以原式可以化为下面这样

$https://latex.codecogs.com/svg.image?\iint_{D1} \frac{u \ln (1+v)}{\sqrt{1-u}}\left|\frac{\partial(x, y)}{\partial(u, v)}\right| d u d v.$

$https://latex.codecogs.com/svg.image?\left|\frac{\partial(x, y)}{\partial(u, v)}\right|=|| \begin{array}{ll}x_u & x_v \\y_u & y_v\end{array}||=| \frac{u}{(1+v)^2} \mid$

下面来找一找积分区域：
　　原来的积分区域:

　　则 $https://latex.codecogs.com/svg.image?\color{red}{u = x + y}$ 可以看作u在该可行域内的线性规划，易求得u的范围为（0,1）而 $https://latex.codecogs.com/svg.image?\color{red}{v = y / x}$ 则可以看作过远点的直线在该区域内可行的斜率，易得角度为(0,pi/2),所以y的范围为(0，+∞)。

$https://latex.codecogs.com/svg.image?\begin{aligned}&\int_0^1 \frac{\mu^2}{\sqrt{1-\mu}} d \mu \int_0^{+\infty} \frac{\ln (1+v)}{(1+v)^2} d u . \\&\int_0^1 \frac{\mu^2}{\sqrt{1-\mu}} d u \stackrel{\sqrt{1-\mu}=t}{=} \int_1^0 \frac{\left(1-t^2\right)^2}{t} \cdot(-2 t) d t \\&=-2\left(\left.t\right|_1 ^0-\left.\frac{2}{3} t^3\right|_1 ^0+\frac{1}{5}\left.t^5\right|_1 ^0\right) \\&=\frac{16}{15}\end{aligned}$

$https://latex.codecogs.com/svg.image?\begin{aligned}\int_0^{+\infty} \frac{\ln (1+v)}{(1+v)^2} d v &=\int_0^{+\infty} \ln (1+v) d\left(-\frac{1}{1+v}\right) \\&=\left.-\frac{\ln (1+v)}{1+v}\right|_0 ^{+\infty}+\int_0^{+\infty} \frac{1}{\left(1+v^2\right)^2} d v \\&=0-\left.\frac{1}{1+v}\right|_0 ^{+\infty} \\&=1\end{aligned}$

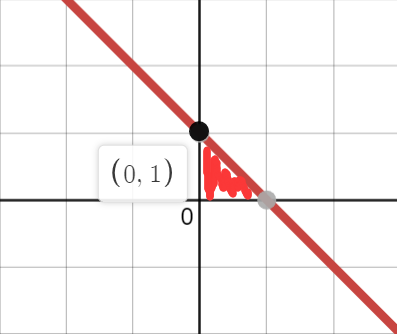
所以答案为16/15
　　下面附上一张参考答案的图：

感谢观看

参考文章:
数学背景知识补充——雅可比矩阵 by Tiger
全国大学生数学竞赛历年真题逐题精讲
 第一届全国大学生数学竞赛预赛试题及解析（非数学类）