KMP算法

KMP —— 一种字符串匹配算法(学习自董晓算法)

给定一个模式串P和一个主串S，求模式串P在主串S中出现的位置。（字符串下标均从1开始）

1. 去最长的想等前后缀，可以保证不漏解
2. 通过模式串前后缀的自我匹配长度，计算next函数（降低事件复杂度的关键），给j指针打一张表，失配时跳到next[j]的位置继续匹配。

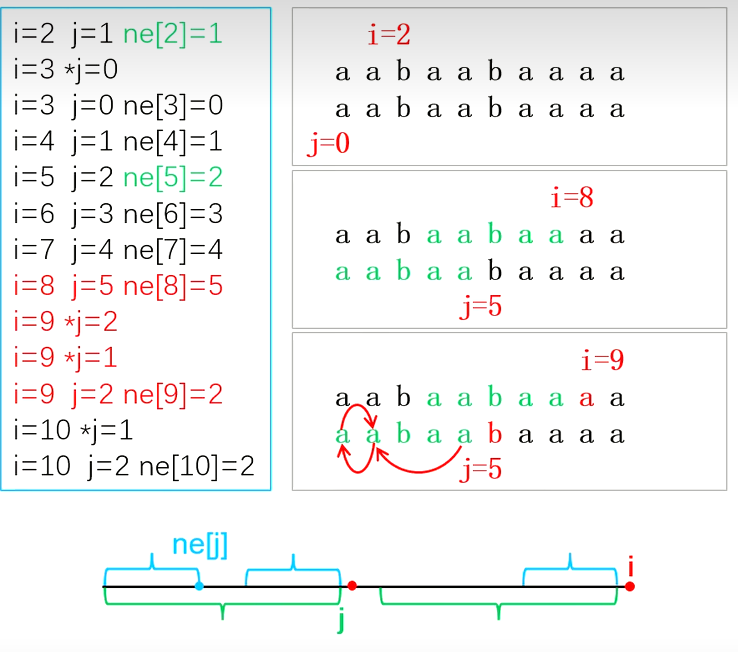
next函数
next[i]表示模式串P[1,i]中相等前后缀的最长长度

next数组代码

ne[1] = 0;
for (int i = 2,j = 0; i <= n; i++) {
	while (j && p[i] != p[j + 1])
		j = ne[j];
	if (p[i] == p[j + 1])
		j++;
	ne[i] = j;
}

双指针： i扫描模式串, j扫描前缀。
初始化，ne[1]=0,i=2,j=0.(固定的)
每轮for循环，i向右走一步。

1. 若p[i]!=p[j+1],让j回跳到能匹配的位置，如果找不到能匹配的位置，j跳回0.
2. 若p[i]==p[j+1],让j+1，指向匹配前缀的末尾。
3. next[i]=j.
4. j指针所走的总步数就决定乐总的执行次数，每轮for，j至多+1，那么j一共向右至多走n步，往左挑的部署加起来不超过n步，否则j变为负数，故j的总步数不会超过2n。例 a–ab.所以时间复杂度O(n)

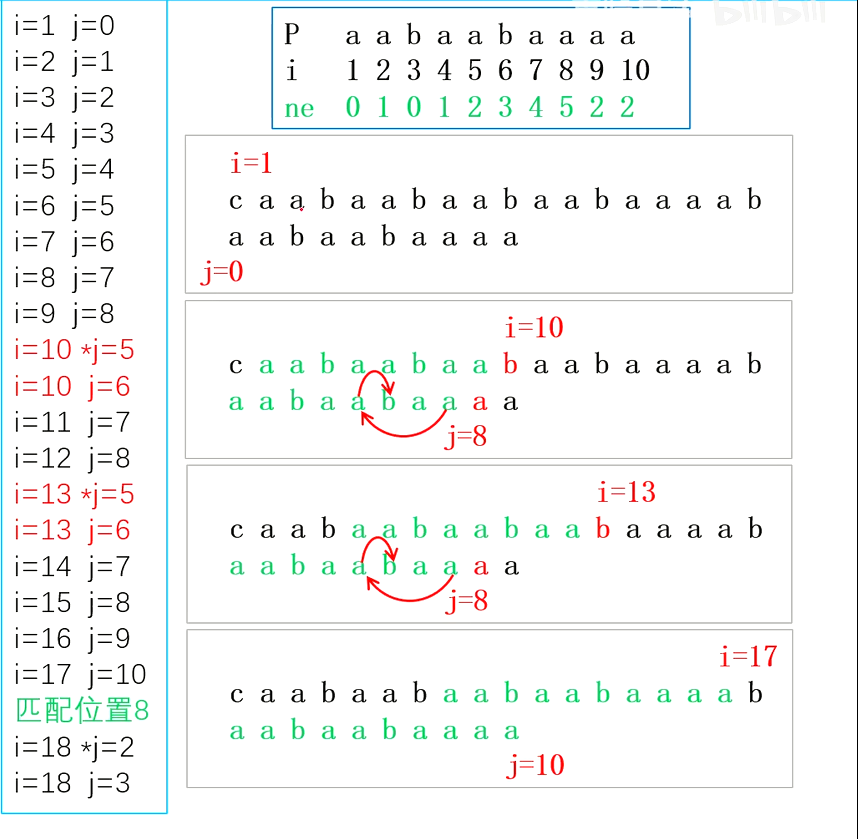
模式串与主串匹配代码

for(int i = 1, j = 0; i <= m; i++) {
        while(j && S[i] != P[j+1]) 
        	j = ne[j];
        if(S[i] == P[j+1]) 
        	j ++;
        if(j == n) 
        	printf("%d\n", i-n+1);
    }

双指针: i扫描主串，j扫描模式串。
初始化，i=1，j=0.
每轮for，i向右走一步。

1. 若s[i]!=p[j+1],让j回跳到能匹配的位置，如果找不到能匹配的位置，j回跳到0.
2. 若s[i]==p[j+1],让j向右走一步。
3. 若匹配成功，输出匹配位置。
4. 时间复杂度同样是O(n)

完整代码

#include <cstring>
#include <iostream>
#include <algorithm>
#include <cstdio>
using namespace std;

const int N = 100;
int m, n;
char S[N], P[N];
int ne[N];

int main(){
    cin >> S+1 >> P+1;
    m = strlen(S+1), n = strlen(P+1);
    // 计算next函数
    puts(S);
    puts(P); 
    //printf("%d %d",m ,n);
    ne[1] = 0;
    for(int i = 2, j = 0; i <= n; i ++){
        while(j && P[i] != P[j+1]) j = ne[j];
        if(P[i] == P[j+1]) j ++; 
        ne[i] = j;
    }
    // KMP匹配
    for(int i = 1, j = 0; i <= m; i ++){
        while(j && S[i] != P[j+1]) j = ne[j];
        if(S[i] == P[j+1]) j ++;
        if(j == n) printf("%d\n", i-n+1);
    }
    for(int i = 1; i <= n; i ++)
        printf("%d ", ne[i]);
    return 0;
}